Multivariate Binary Representation
In this blog post, I introduce Multivariate Binary Representation: A method for encoding the binary expansions of integers as multivariate monomials using a polynomial quotient ring. This encoding process involves modular exponentiation within a specific ring structure, referred to as ![]() , to uniquely represent any positive integer
, to uniquely represent any positive integer ![]() .
.
Let ![]() . Consider the recursive polynomial quotient ring [1]
. Consider the recursive polynomial quotient ring [1]
![]()
where the ideal
![]()
In ![]() , we adopt the dlex monomial ordering
, we adopt the dlex monomial ordering ![]() . Within the ring
. Within the ring ![]() , the variables
, the variables ![]() satisfy the recursive relation
satisfy the recursive relation ![]() for
for ![]() , where
, where ![]() refers to the next variable in the sequence, and
refers to the next variable in the sequence, and ![]() .
.
Encoding
Expanding ![]() in
in ![]() gives a unique combinatorial representation of
gives a unique combinatorial representation of ![]() as a monomial in variables
as a monomial in variables ![]() . Consider
. Consider ![]() . The expansions for
. The expansions for ![]() are given below:
are given below:
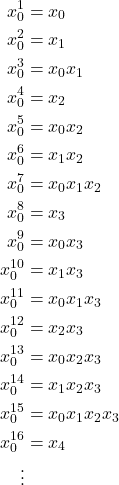
To clarify, on the righthand side we have taken ![]() modulo the ideal
modulo the ideal ![]() .
.
Notice that the ![]() within the expansion of
within the expansion of ![]() correspond to the positions of
correspond to the positions of ![]() bits in the binary expansion of
bits in the binary expansion of ![]() .
.
Example: Encoding.
Consider ![]() . Here, we have
. Here, we have ![]() . Expanding
. Expanding ![]() in our ring
in our ring ![]() gives
gives
![]()
We compare the above result to the binary expansion of ![]() , which is
, which is
![]()
Decoding
To convert ![]() back to binary, the simplest method is to enumerate the indices of the variables in the monomial and sum the corresponding powers of two.
back to binary, the simplest method is to enumerate the indices of the variables in the monomial and sum the corresponding powers of two.
Example: Decoding.
Let ![]() , hence
, hence ![]() . To decode, we compute
. To decode, we compute ![]() . Summing the corresponding powers of two for
. Summing the corresponding powers of two for ![]() yields
yields
![]()
Unusual Properties of 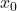 in
in 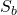
The element ![]() in the ring
in the ring ![]() possesses unusual root extraction and discrete logarithm properties. In
possesses unusual root extraction and discrete logarithm properties. In ![]() , each power
, each power ![]() corresponds uniquely to a multivariate monomial modulo the ideal
corresponds uniquely to a multivariate monomial modulo the ideal ![]() . This mapping provides an analogy to the discrete logarithm
. This mapping provides an analogy to the discrete logarithm
![]()
where ![]() is the unique combinatorial representation of the integer
is the unique combinatorial representation of the integer ![]() . Just as the discrete logarithm function uniquely determines the exponent in modular arithmetic,
. Just as the discrete logarithm function uniquely determines the exponent in modular arithmetic, ![]() uniquely determines
uniquely determines ![]() in
in ![]() .
.
Another potentially interesting property is that ![]() serves as the
serves as the ![]() -th root of all integers
-th root of all integers ![]() within the range
within the range ![]() . Specifically,
. Specifically, ![]() is the
is the ![]() -th root of the element representing
-th root of the element representing ![]() in
in ![]() . For instance,
. For instance, ![]() is the
is the ![]() th root of
th root of ![]() in
in ![]() :
:
![]()
The utility of these properties remains an open question for now.
Source Code
Below is Sage code which encodes and decodes a range of integers to multivariate binary, printing the results in CSV format.
# Joseph Shunia, (C) 2024
n_min, n_max = 1, 16
b_max = floor(log(n_max,2))+1
R = PolynomialRing(ZZ, b_max+1, 'x')
x = R.gens()
I_list = [x[i]^2 - x[i+1] if i < b_max else x[i]^2 for i in range(b_max + 1)]
subs_dict = {x[i]: 2^i for i in range(b_max + 1)}
I = R.ideal(I_list)
G = I.groebner_basis()
S = R.quotient(I, 'x')
def mvb_encode(n):
return S(x[0]^n)
def mvb_decode(poly):
sum = 0
vars = poly.monomials()[0].variables()
for v in vars:
sum += subs_dict[v]
return sum
print(f'n, encoded, decoded')
for n in range(n_min, n_max+1):
n_encoded = mvb_encode(n)
n_decoded = mvb_decode(n_encoded)
print(f'{n}, {n_encoded}, {n_decoded}')
If you want to run the code in your browser, you can use SageCell.
Related Works
Multivariate binary representation shares similarities to Boolean polynomials [2], which are defined over the ring ![]() , where the ideal
, where the ideal ![]() .
.
A fundamental difference is that an integer ![]() is encoded to multivariate binary representation by way of exponentiation, whereas the encoding process is performed manually for Boolean polynomials by examining the binary expansion of
is encoded to multivariate binary representation by way of exponentiation, whereas the encoding process is performed manually for Boolean polynomials by examining the binary expansion of ![]() (similar to how our decoding process is performed). Also, in multivariate binary, the encoded representation is a single monomial, as opposed to a sum of monomials. Furthermore, in Boolean polynomials, all coefficients are taken modulo
(similar to how our decoding process is performed). Also, in multivariate binary, the encoded representation is a single monomial, as opposed to a sum of monomials. Furthermore, in Boolean polynomials, all coefficients are taken modulo ![]() , which is not necessarily the case in the ring
, which is not necessarily the case in the ring ![]() .
.
To illustrate these differences, here is the encoded representation of ![]() as a Boolean polynomial:
as a Boolean polynomial:
![]()
where the function ![]() performs the encoding by examining the binary expansion of
performs the encoding by examining the binary expansion of ![]() .
.
Further Reading
If you would like to learn more about recursive polynomial quotient rings and their applications, please see my recent preprint [1], which is available on arXiv: A Polynomial Ring Connecting Central Binomial Coefficients and Gould's Sequence.
In the paper, I give a formal definition of a "recursive polynomial quotient ring", and demonstrate how a specific variation of the construction generates the terms of two famous integer sequences: The central binomial coefficients ![]() (A000984) and Gould's sequence (A001316).
(A000984) and Gould's sequence (A001316).
[1] Joseph M. Shunia, A Polynomial Ring Connecting Central Binomial Coefficients and Gould's Sequence, arXiv:2312.00302 [math.GM], 2023.
[2] Michael Brickenstein and Alexander Dreyer, PolyBoRi: A framework for Gröbner-basis computations with Boolean polynomials, Journal of Symbolic Computation, Volume 44, Issue 9, 2009.
Comments are closed.