An Easy Formula for Prime Numbers
A current research goal of mine is to find an elementary formula (arithmetic term) for the ![]() -th prime number. Today, I can at least report some partial progress.
-th prime number. Today, I can at least report some partial progress.
To provide some initial context: An arithmetic term is defined as an expression which uses only the elementary arithmetic operations: ![]() (*).
(*).
(*) For a precise definition, please see my recent preprint: Elementary Formulas for Greatest Common Divisors and Semiprime Factors.
While a few formulas for primes are known, none can be transformed into an arithmetic term, and all seem to exploit Wilson’s theorem: ![]() , if and only if
, if and only if ![]() is prime.
is prime.
Seemingly, finding an arithmetic term for the ![]() th prime is an incredibly difficult task. Indeed, this quest has baffled some of the greatest minds in human history.
th prime is an incredibly difficult task. Indeed, this quest has baffled some of the greatest minds in human history.
“Mathematicians have tried in vain to this day to discover some order in the sequence of prime numbers, and we have reason to believe that it is a mystery into which the human mind will never penetrate” – Leonhard Euler.
After discussing the problem with fellow researchers, it occurred to me that there is indeed a rather “easy” formula which generates the sequence of primes in order, albeit with some repetitions.
Define ![]() to be an integer-valued function which returns the greatest prime
to be an integer-valued function which returns the greatest prime ![]() . Then
. Then
(1) 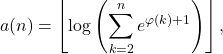
where ![]() represents Euler’s totient function.
represents Euler’s totient function.
Starting from ![]() ,
, ![]() yields the sequence terms (A007917 in the OEIS):
yields the sequence terms (A007917 in the OEIS):
![]()
![]() .
.
Explanation
When ![]() is prime,
is prime, ![]() . Now, consider the polynomial function
. Now, consider the polynomial function
(2) ![Rendered by QuickLaTeX.com \begin{align*} f_n(x) = \sum_{k=2}^{n} x^{\varphi(k)+1} \in \mathbb{Z}[x] . \end{align*}](https://www.josephshunia.com/wp-content/ql-cache/quicklatex.com-12f2e950666c5813d39db2399cf6258d_l3.png)
In this case, ![]() , the greatest prime
, the greatest prime ![]() . This is because
. This is because ![]() if and only if
if and only if ![]() is prime. Thus, the maximal value for
is prime. Thus, the maximal value for ![]() will be a prime number, and this is exactly the largest prime
will be a prime number, and this is exactly the largest prime ![]() . Evaluating
. Evaluating ![]() , and taking the floor of the natural logarithm yields the desired result. For a rigorous proof, there are some additional details to consider. However, I omit those for now and plan to include them in an upcoming paper.
, and taking the floor of the natural logarithm yields the desired result. For a rigorous proof, there are some additional details to consider. However, I omit those for now and plan to include them in an upcoming paper.
Update: I have posted an attempt at a semi-rigorous proof of the formula on my personal Github page: see here. I will caution that the proof has not yet been reviewed.
Implications and Future Research
Recently, researchers Prunescu and Sauras-Altuzarra released a preprint [6] which gives an arithmetic term for Euler’s totient function ![]() . Their formula is enormous and impractical, but I believe the result is incredible: It demonstrates that even something as complicated as Euler’s totient function can be expressed using only elementary arithmetic. The techniques used in the paper of Prunescu and Sauras-Altuzarra are derived from Matiyasevich’s (1970) [1] solution to Hilbert’s tenth problem, as well as the subsequent works of Mazzanti (2002) [2] and Marchenkov (2006) [3] regarding computability and Kalmar elementary functions. Applying a similar approach, it seems feasible to convert the formula
. Their formula is enormous and impractical, but I believe the result is incredible: It demonstrates that even something as complicated as Euler’s totient function can be expressed using only elementary arithmetic. The techniques used in the paper of Prunescu and Sauras-Altuzarra are derived from Matiyasevich’s (1970) [1] solution to Hilbert’s tenth problem, as well as the subsequent works of Mazzanti (2002) [2] and Marchenkov (2006) [3] regarding computability and Kalmar elementary functions. Applying a similar approach, it seems feasible to convert the formula ![]() to an arithmetic term.
to an arithmetic term.
The collective works of Mazzanti, Marchenkov, Matiyasevich, along with the earlier works of Julia Robinson [4] (1952), tell us that there exists an arithmetic term for the ![]() -th prime number. While the function
-th prime number. While the function ![]() gives some nice progress, it is not straightforward to convert it to a direct formula for the
gives some nice progress, it is not straightforward to convert it to a direct formula for the ![]() -th prime number. Nor is it clear if it is even possible to do so without substantial changes. While the formula is known to exist, one should reasonably expect that it is extremely large and impractical, requiring many pages to write down in full. Hence, the problem remains difficult. Though, perhaps it is easier than we think!
-th prime number. Nor is it clear if it is even possible to do so without substantial changes. While the formula is known to exist, one should reasonably expect that it is extremely large and impractical, requiring many pages to write down in full. Hence, the problem remains difficult. Though, perhaps it is easier than we think!
References
[1] Yuri Matiyasevich. (1970), The Diophantineness of Enumerable Sets, Doklady Akademii Nauk SSSR.
[2] Stefano Mazzanti. (2002), Plain Bases for Classes of Primitive Recursive Functions, Mathematical Logic Quarterly.
[3] Sergey S. Marchenkov. (2007), Superpositions of Elementary Arithmetic Functions, Journal of Applied and Industrial Mathematics.
[4] Julia Robinson. (1952), Existential Definability in Arithmetic, Transactions of the American Mathematical Society.
[5] Yuri Matiyasevich. (1999), Formulas for Prime Numbers, Kvant Selecta: Algebra and Analysis, vol. II, American Mathematical Society, pp. 13–24, ISBN 978-0-8218-1915-9.
[6] Mihai Prunescu and Lorenzo Sauras-Altuzarra. (2024), On the Representation of Number-Theoretic Functions by Arithmetic Terms, arXiv preprint.
SHA256:
98224c57dbb0e7b1012084c1729e0b19f684d6e2eda4fef2096c22e1d45bb6b1
9638bd19497819f3f9bfea74cbf805a81a116854ddc6b95c6a0cfeb1e1a8117b