On the n-th decimal digit of pi

Published on October 23, 2024

Define the integer-valued function $\pi_{10}(n)$ to return the $n$ -th decimal digit of $\pi$ . This is the sequence A000796 in the OEIS.

We will now state a conjecture that is inspired by a limit appearing in an elementary proof of Stirling’s approximation by Jakub Smolík [1]. In his proof, Smolík shows:

$\begin{align*} \frac{\pi}{2} = \lim_{n\rightarrow\infty} \frac{2^{4n} n!^4}{(2n)!^2 (2n+1)} . \end{align*}$

Conjecture. Let $n,k \in \mathbb{Z}^+$ such that $k \geq (6n)^{n}$ . Then, the $n$ -th decimal digit of $\pi$ , denoted as $\pi_{10}(n)$ , is given by the expression:

$\begin{align*} \pi_{10}(n) = \left\lfloor \frac{10^n 2^{4k+1} (k!)^4}{(2k)!^2 (2k+1)} \right\rfloor \bmod 10 . \end{align*}$

We offer a partial proof of this conjecture:

Considering the term within the floor function, we can rewrite it as

$\begin{align*} \frac{\pi 2^{n-1} 5^n (2k+1) \Gamma(k+1)^2}{\Gamma(k+3/2)^2} \end{align*}$

We observe that

$\begin{align*} \lim_{k\to\infty} \frac{(2k+1) \Gamma(k+1)^2}{\Gamma(k+3/2)^2} = 2 . \end{align*}$

$\begin{align*} \lim_{k\to\infty} \frac{\pi 2^{n-1} 5^n (2k+1) \Gamma(k+1)^2}{\Gamma(k+3/2)^2} = \pi 2^{n-1} 5^n (2) = 10^n \pi . \end{align*}$

Thus, by choosing $k$ sufficiently large, we can extract the $n$ -th decimal digit of $\pi$ as

$\begin{align*} \left\lfloor \frac{10^n 2^{4k+1} (k!)^4}{(2k)!^2 (2k+1)} \right\rfloor \bmod 10 = \pi_{10}(n). \end{align*}$

It remains only to prove that $k \geq (6n)^{n}$ is large enough to ensure that the formula holds for all $n$ .

An arithmetic term is a fixed-length elementary closed form expression, applicable to all $n$ , which uses only the operations of addition, multiplication, bounded subtraction, division with remainder, and exponentiation.

Our representation of the $n$ -th decimal digit of $\pi$ constitutes an arithmetic term. The fact that our formula contains factorials may seem to rule this out, however,
we can rewrite our formula for $\pi_{10}(n)$ using the arithmetic term for factorials below:

$\begin{align*} k! = \left\lfloor \frac{(k+1)^{k(k+2)}}{\left\lfloor \frac{\left( (k+1)^{k(k+2)} + 1 \right)^{(k+1)^{k+2}}}{(k+1)^{k^2(k+2)}} \right\rfloor \bmod (k+1)^{k(k+2)}} \right\rfloor \end{align*}$

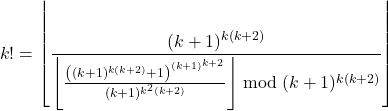
The above factorial formula is derived from results of Julia Robinson [2], who first showed that

$\begin{align*} \lim_{r\to\infty} r^k / \binom{r}{k} = k! \end{align*}$

and for $r \geq (k+1)^{k+2}$ :

$\begin{align*} \left\lfloor r^k / \binom{r}{k} \right\rfloor = k! . \end{align*}$

References

[1] J. Smolík. “An Elementary Proof of Stirling’s Formula.” arXiv preprint arXiv:2310.04872. URL https://arxiv.org/pdf/2310.04872 (2023).
[2] J. Robinson. “Existential definability in arithmetic.” Transactions of the American Mathematical Society (1952).

josephshunia

Categories:

conjectures

discoveries

formulas

Comments are closed.