Strange Formulas for Binomial Coefficients
Binomial coefficients have long been an obsession of mine, since my earliest days of studying the integers, when I naively rediscovered Pascal’s triangle through simple counting. These unassuming numbers, often written as ![]() , have a surprising depth and elegance that never cease to amaze me.
, have a surprising depth and elegance that never cease to amaze me.
For those who may be unfamiliar, binomial coefficients are the coefficients of the terms in the expansion of the binomial expression ![]() . They also represent the number of ways to choose
. They also represent the number of ways to choose ![]() objects from a set of
objects from a set of ![]() objects, making them fundamental to combinatorics and probability theory. The standard formula for calculating binomial coefficients uses factorials:
objects, making them fundamental to combinatorics and probability theory. The standard formula for calculating binomial coefficients uses factorials:
![]()
In my recent paper, “Polynomial Quotient Rings and Kronecker Substitution for Deriving Combinatorial Identities” (preprint), I explored a new approach for deriving formulas for combinatorial objects such as these. The key idea is to apply Kronecker substitution, a technique for encoding polynomials as integers, to polynomial expansions.
Through this approach, I was able to discover several new formulas for both binomial coefficients ![]() and central binomial coefficients
and central binomial coefficients ![]() . Included below are some of the most surprising results.
. Included below are some of the most surprising results.
Binomial Coefficients ![]() :
:
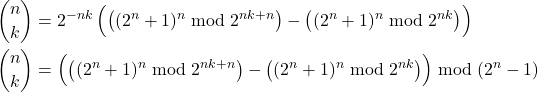
Central Binomial Coefficients ![]() :
:
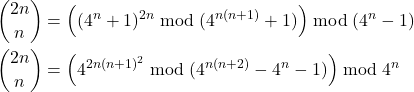
Central Binomial Coefficients congruence ![]() :
:
![]()
Partial Sums of Binomial Coefficients:
Let ![]() such that
such that ![]() . Then
. Then
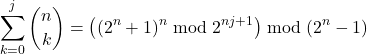
and
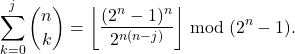
Let ![]() such that
such that ![]() . Then
. Then
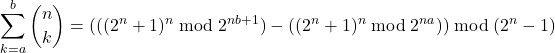
If you’re as fascinated by these formulas as I am, I invite you to read my paper for a detailed explanation of the underlying mathematics.