Those primes and omega
On the 31st of October 2024, Mihai Prunescu gave a talk at the Logic Seminar in Bucharest presenting the results of our recent collaboration. This talk was entitled: “Primes Resurrection on Halloween”.
Our collaboration pertains to an arithmetic term approach to the prime numbers. In the spirit of Halloween, I will leave it somewhat mysterious for now, but let’s just say: I am extremely excited to share the results and I hope that you will find them as incredible as I do! The paper is finished and in its final stages of proofreading and internal verification. Barring any unforeseen issues, I anticipate that the preprint will be made available by the end of this month.
In the meantime, I would like to offer a sneak preview of a result from our paper: An arithmetic term for the omega function ![]() , which counts the number of distinct prime divisors of
, which counts the number of distinct prime divisors of ![]() . This is the OEIS sequence A001221. Starting from
. This is the OEIS sequence A001221. Starting from ![]() , it begins as
, it begins as
![]()
The following arithmetic terms are used in Mazzanti [1]:
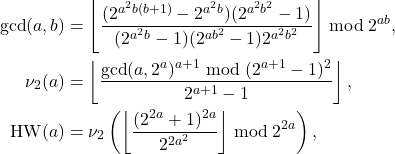
where ![]() returns the Hamming weight of
returns the Hamming weight of ![]() , and
, and ![]() returns the highest exponent of
returns the highest exponent of ![]() dividing
dividing ![]() .
.
We define the arithmetic term:
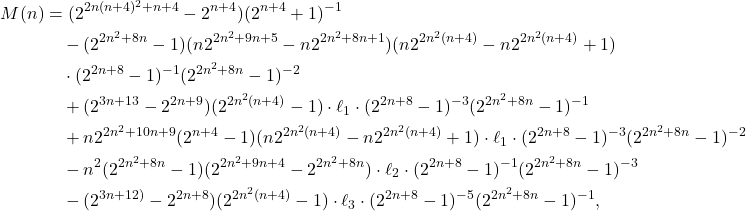
where

Theorem. For all ![]() , one has
, one has
![]()
This immense formula is difficult to appreciate. To maintain the air of mystery, I omit the proof for the moment. This result and its proof will be included in our forthcoming preprint.
References
[1] Stefano Mazzanti. (2002), Plain Bases for Classes of Primitive Recursive Functions, Mathematical Logic Quarterly.
[2] Mihai Prunescu and Lorenzo Sauras-Altuzarra. (2024), An Arithmetic Term for the Factorial Function, Examples and Counterexamples.
Comments are closed.